Inaugural lecture

The following presentation is also available in Powerpoint and PDF formats. The three movies are provided separately in QuickTime format: Schelling.mp4 (14.2 MB), GeoSim.mov (27.3 MB), and GeoSim3D.mp4 (44.5 MB). Everything can also be downloaded as one large Zip archive (27.2 MB).

I will start on a personal note. When I entered the PhD program in political science at the University of Michigan in September 1990, the Berlin wall had come down half a year earlier. At the end of my first year, the Soviet Union collapsed. It was, to say the least, a time of flux.

And it still is today. Like in the period immediately after WWII, we can only dimly discern the new fault-lines of world politics.

Obviously, any student of international relations and conflict research has to shoot at a moving target. Unlike atoms and physical laws, the social world is steadily evolving, sometimes by leaps and bounds. This is what makes it so hard to study the complexity of human relations.

As the late Nobel Laureate Herbert Simon once said, for precisely these reasons, the social sciences are the really “hard” sciences.

Yet, our theories of international relations appear curiously static and detached from the revolutionary changes that the world is presently undergoing. This observation remains as valid today as it was immediately after the end of the Cold War.

In this lecture, I will present an alternative way forward based on complexity theory that renders international theorizing more dynamic and context-sensitive.

I will illustrate this approach with snapshots from my own research in order to tell you (1) where I come from intellectually, (2) how far I have gotten, and (3) where I would like to go with my research agenda in the years to come here at ETH.

As an aspiring PhD student, I realized that the conceptual tool bag in political science, which had been adapted to Cold War conditions, was much less suited to the policy challenges that followed after the fall of the Berlin Wall.

In particular, conventional approaches to political science are almost without exception analytical rather than systemic, in the sense that they sub-divide problems into smaller ones in the hope of understanding the whole once the components have been fully grasped. This strategy has proven exceedingly successful in the natural sciences.

But if the bits and pieces hang together in a complex jigsaw and experiments that isolate the parts cannot be performed, this strategy will almost certainly fail.

To see what’s missing from the conventional research agenda, let’s focus on social complexity along three main dimensions, namely time, space, and identity:

Time. Turbulent periods, such as the years following the Cold War, remind us that the normal state of world politics is not stability. States come and go, organizations emerge, unite, split up, and collapse. Indeed, the dissolution of the Soviet Union was not a mere data point; rather, it represented a transition that still hasn’t settled. Yet standard theories still assume that there is a stable cast of actors, and that transitional periods can be neglected. In other words, in our theories, history has dropped out of the picture.

Space. It is equally unfortunate that territorial space tends to be overlooked by scholars of world politics. Indeed, it is hard to think of any realm that is more deeply spatial than territorial relations among states, and territory continues to matter powerfully in spite of globalization. For sure, it matters to the Pentagon that Iraq is on the other side of the world. But in our theories, context-free variables without physical extension have replaced the wheres and whens of geopolitics.

Identity. Finally, and equally seriously, the important issue of identity has typically been swept under the theoretical rug. Given the influence of materialist thinking during the Cold War, reinforced by American social science, this is hardly surprising, but nonetheless troubling, because political mobilization and conflict often depend on identities. Indeed, it is hard to make sense of the Soviet collapse without reference to the power of cultural symbols, especially nationalist ones.

The result of this triple neglect has been a tendency to cut history into small pieces, feeding them into models and regression equations that produce ostensibly general results.

Instead of merely studying the effect of general variables in separate cases, it is also helpful to consider the entire system as a complex configuration along the three dimensions of time, space, and identity.

How can we bring these dimensions back into theorizing and model-building?

Fortunately, classical sociology offers an alternative viewpoint, especially the research tradition known as sociological process theory. Simmel’s theory of Vergesellschaftung explicitly theorizes these three dimensions of complexity. Rather than taking large-scale social groups for granted, he investigated how they manage to survive despite their long historical duration, their vast spatial extension, and the large number of people involved.

Although inspiring, this research tradition needs to be complemented with more precise tools. Given the massive complexity of macro-historical processes, there is a need for an “accounting mechanism” that assists the theorist in conducting thought experiments.
Formal models help theory-builders sharpen abstract concepts and articulate otherwise hard-to-grasp mechanisms.
The crux, however, is that most conventional modeling techniques are not really up to the three-dimensional challenge that I have just sketched.

Among available macro approaches, the most obvious choice would fall to dynamic simulation in the global modeling tradition. Such macro models, which were especially popular in the 1970s following the pessimistic report Limits to Growth, trace a large number of macro variables over time and typically attempt to predict population and economic trends many years, sometimes even decades, into the future.

By the early 1990s, however, the method had fallen in disrepute, mostly due to its overly ambitious predictive claims. Moreover, the methodology also stumbles on the spatial and identity dimensions, despite offering excellent tools to grapple with dynamics.

Fortunately, inter-disciplinary advances in complexity theory provide new foundations for theory-building that circumvent some of these difficulties.

Complexity theorists study complex adaptive systems that exhibit properties that emerge from local interactions among many, typically heterogeneous agents mutually constituting their own environment.

Note that the emergent macro patterns can be produced by very simple micro-level rules. Here are two examples:

Researchers have tried to explain birds’ swarming behavior by creating artificial computerized “boids” that follow a very small number of rules of thumb, or perhaps we should say, rules of wing.
Another example is the attempt to trace the growth of the Internet as a dynamic network. It appears to follow specific statistical properties that result from a snow-balling logic that makes popular sites ever more connected.

Modern statistical physics shows that many diverse processes exhibit powerful and deep similarities at the macro level despite massive differences at the micro level. (This is a much more optimistic message than that of chaos theory.)

Such analogies may enable us to transfer knowledge about one realm of complexity to a different one, as the physicists have done in the case of fluids and magnets.

If -- and this is far from obvious -- social systems are governed by similar principles, then we could learn from complexity theory as developed in the natural sciences to uncover processes and mechanisms that operate in world politics.

I am aware that it sounds like a breathtakingly optimistic and naïve endeavor to use physical particle systems as a guide to the messy realities of world politics. Indeed, there is something deeply distasteful about treating people, with all their dreams and imaginations, as if they were mere particles.

What about free will? What about the accidents of history? Didn’t the length of Cleopatra’s nose change the course of world history? After all, it may be true that history is just one damned thing after the other.

Yet I will ask you to suspend your skepticism and disbelief at least for a few moments.

So far, my lecture has been quite abstract. So instead of trying to convince you in very general terms that complexity theory may have something to say about the social world, let me give you a concrete example.

Urban planning, or rather the lack thereof, is a great way to visualize these abstract principles at work

If you ever doubted this, I would recommend that you pay a visit to the Berlin television tower. From there you can see the spatial manifestation of two very different socio-economic systems. On the eastern side, the unmistakable contours of decades of central planning are visible.

In the west, however, everything looks quite chaotic, but is it really that chaotic? In fact, there seems to be an order to the madness. In American cities, for example, ethnicity changes abruptly as you move from one neighborhood to another.

This cultural diversity is what makes US cities such exciting places to visit. Still, we have to ask why the boundaries between the neighborhoods are so sharply defined in spite of the almost total lack of city-planning. How could this segregated order emerge from a myriad of moves without city planning?

Thomas Schelling, an American economist, was puzzled by this pattern and decided to build a model to show how neighborhood segregation could emerge through unplanned interactions of micro-level actions.

Of course, segregation would not be so hard to explain if it stemmed from truly racist individuals. Yet Schelling suspected that the explanation is much more subtle than that.

Writing in the late 1970s at the dawn of the age of personal computers, Schelling set out to solve this problem equipped with a table of random numbers, a checker board, a bunch of coins, as well as equal measures of patience and curiosity.

Having placed his pennies and dimes randomly on the board, leaving a few vacancies, the famous economist now gave the coins the opportunity to move according to very simple rules:

If a penny found that at least a third of the inhabitants in the immediate neighborhood were also pennies, there would be no reason to move. With less than the critical third, however, the penny would decide to move to another randomly selected site where it would be surrounded by enough pennies. The corresponding rule would also apply to the dimes.

Notice that our friends the pennies and dimes hardly deserve to be called racists. Their desire not to live in isolated pockets seems quite reasonable.

What is the result of this exercise? Based on these weak assumptions, will neighborhood segregation ever emerge?

Fortunately, we don’t have to use pennies and dimes to find out, but can rely on the power of a PC. Instead of using coins, let us instead represent the two communities as the red and blue people.

All in all, there are 30 by 30 sites, out of which 90% are occupied and divided into 450 of each type.

In addition, there are going to be 10% vacant sites, here shown in black.

Note that all these sites are randomly mixed. Despite this initial randomness, will segregation result?

>> Sample run 1

>> It takes some time for the inhabitants to sort out what they want.

>> There is a fair amount of moving back and forth.

But slowly but surely, what emerges is a stunning segregation pattern! Schelling’s intuition was right. Segregation emerges through self-organization even among relatively tolerant individuals.
>> This is a very robust result.

What I have just shown you is a particularly simple instance of a general computational modeling strategy that is called agent-based modeling. It allows researchers to create, analyze, and experiment with, artificial worlds populated by agents that interact in non-trivial ways and that constitute their own environment.

Such models often produce emergent effects, i.e. outcomes that are truly systemic and that cannot be reduced to properties of the system’s components, as for example the segregation pattern we just generated.

It’s possible to measure emergent effects. The segregation model produces two important results:

First of all there is a massive reduction of the number of neighborhoods, in this case, from 155 at the beginning down to a mere 16.
Furthermore, the overall happiness in the system, measured as the proportion of content inhabitants, increases from about 80% to a state in which nobody has an incentive to move. This is a global equilibrium.

Thus, through local, adaptive steps, the system as a whole manages to find an equilibrium. (Obviously there may be normative reasons to be unhappy with this segregated outcome, but at least all individuals are satisfied in a narrow sense!)

At this point, let’s return to our three dimensions of complexity:

Time. Rather than trying to describe a given equilibrium, Schelling’s model traces how an equilibrium is reached through many small steps. Thus, what’s important is how to get to a specific outcome rather than to characterize it once it has materialized.
Space. As opposed to conventional methodology, Schelling’s model offers an explicit representation of spatial relationships [because, as the real estate agents say, what matters in this business is: location, location, location].
Identity. Finally, there are two distinct types of actors, the blue and the red people, and their behavior is directly dependent on the identity of their neighbors. One important advantage of agent-based models is precisely that they allow for the depiction of highly diverse actors.

It would thus seem that Schelling’s model points in the right direction. Yet, it doesn’t say much about war and peace.

I therefore have to demonstrate that the leap from urban neighborhoods to warfare among states is not as a long as it may seem.

We have already seen how the segregation process in Schelling’s model reduces the number of neighborhoods drastically.

By analogy a similar phenomenon actually happened in Europe with respect to the number of states on our continent. At the end of the Middle Ages, there were scores of independent or semi-independent geopolitical units in Europe. Depending on how one defines them, it is possible to count to half a thousand such units in 1500.

In fact, this is what the political map looked like. This is quite an impressive patchwork, especially Germany and Italy.

Four hundred years later, the picture looks very different! The number of states has now gone down drastically to two dozens.

What explains this extraordinary development? Although historians, sociologists and political scientists are still debating this issue intensively, most of them agree that this has something to do with warfare.

As Charles Tilly has put it in an elegant aphorism: “States made war and war made the state.”

Impressed by this dynamic story, I set out to create an artificial geopolitical system that mimics the process of competitive state formation. Rather than trying to capture international politics in terms of a set of laws operating in a timeless manner, my idea was to treat the topic as a geopolitical process unfolding at the macro level.

More specifically, let us start with a large number of states and then let combat and conquest weed out the losers, thus creating a consolidated map like early 20th century Europe.

Already in 1977, Bremer and Mihalka introduced a model of geopolitical competition. It features state-like organizations with dynamic borders that grow through conquest.

This model became an important source of inspiration in my own dissertation research. I decided to construct a geopolitical system in this tradition but starting from scratch. This is how Geosim came about.

Geosim is a family of agent-based models that is based on a dynamic network of interstate relations superimposed on a square grid. All interactions are local, between adjacent states. Unlike Schelling’s inhabitants, however, the main protagonists here are more complex, hierarchical states.

Each state capital can absorb and dominate a number of provinces in a perfectly Hobbesian fashion [see the dots]. Moreover, their borders are sharply defined [see the lines]. Finally, they derive their power from the number of provinces they control -- thus, the larger a state is, the more powerful it is.

>> Sample run 2 Geosim

Here we have 200 sovereign states.

What happens if we unleash these little power-hungry fellows?

Will one state manage to take over the entire system? After all, in the European case, both Napoleon and Hitler got rather close to this outcome.

Combat follows if the local power balance exceeds a preset threshold in favor of the attacker. In this case, a challenger has to be exactly twice as powerful as its opponent to launch an attack. The potential victims, who are vulnerable to invasion are here shown in red.

What do we observe?

First of all, the number of states declines drastically.
Moreover, conquest happens frequently, which leads to complete and partial state disintegration when the capital loses control over its territories.
Perhaps most surprisingly, in this run, a stable equilibrium results with as many as 15 states results rather than one state taking over the entire system.

As with Schelling’s model, it is possible to measure the development of the system over time.

Instead of neighborhoods, we trace the decline in the number of states over time. A declining, irregular pattern appears. [see left graph]

The increase in security is not a regular one either. Indeed, the proportion of secure areas, measured in terms of the number of red, unthreatened sites, exhibits an even more jagged curve pointing upwards. Clearly the states become more secure over time.

Rem. It should be noted that security in this Hobbesian sense may be less than normatively appealing, because we are counting conquered provinces inside unthreatened states as secure. This amounts to the same security as prey feel inside the belly of the predator.

Of course, we cannot draw any conclusions based on a single run. This is a highly random system, so we need to regenerate many artificial worlds.

If we rerun this particular model while varying the details, a great variety of outcomes materializes:

First I show you the final outcome of the sample run.
There are many other examples of multipolar systems with fewer states, as this example with seven states.
There are bipolar systems that look like simplified versions of the Cold War.
And there are unipolar ones that resemble Europe had Napoleon or Hitler prevailed.

Despite this variety, the analogies to Schelling’s model should be clear:

First, the processes reach equilibrium through self-organization.
Second, there is a reduction of collective units, in Schelling’s case neighborhoods, and in Geosim, states.
Third, the system adapts by making the individual units more satisfied or secure.

Of course there are important differences too:

Whereas Schelling’s model features moving individuals, in my model adjustment happens through moving borders as a result of conquest
Convergence in the geopolitical case is less even and includes reversals.
As opposed to the segregation model, this simple version of Geosim doesn’t feature distinct identities.

Now that we have familiarized ourselves with the core logic of the model, it is time to introduce a bit more realism.

So far we have focused on processes that end in a stable equilibrium, but in world history, there is no end in sight. Thus we should be at least as interested in studying on-going processes as exploring specific configurations.

Moreover, it is possible to ask for a closer fit with the phenomenon in question, whether it is a configuration or a process. We may want to reproduce entire probability distributions of properties rather than merely qualitative characteristics.

If we combine these possibilities, we get four types of emergent phenomena that fit into a 2 x 2 table.

The sample runs that I just showed you both belong to the lower right cell, here labeled 3.

I will now invite you to a very quick guided tour illustrating what Geosim is capable of. Obviously we will not be able to study each model in any detail, but I hope this survey will give you a flavor of the possibilities.

Moving clock-wise from the upper left corner, I will start by considering Example 1, which features war-size distributions. This case requires the researcher to reconstruct the distributional profile of an on-going process.

Since Richardson’s pioneering efforts to collect quantitative data about conflict processes in the 1940s, we know that war sizes are power-law distributed. Using logarithmic axes, the diagram plots cumulative war frequencies as a function of war size. A straight line in a log-log plot suggests the presence of a power law.

While such distributions could emerge in many different ways, the notion of self-organized criticality provides clues about a plausible set of mechanisms.
In general, outcomes of this type are typically generated by non-equilibrium processes building up tension within slowly driven non-linear systems. When the tension is released, the outbursts conform with power-law distributions, not unlike earthquakes. The late Danish physicist Per Bak used a sandpile as a paradigmatic example of this type of systems.

What are the geopolitical mechanisms that generate this pattern? To find out, I modified Geosim to produce realistically distributed war sizes. My idea was to let technological change play the role of the steady trickle of sand. The repeated introduction of technical innovations creates strategic opportunities that states will exploit to expand their territories. Warfare in different sizes emerges as a side-effect of this process.

Here is a simulated war-size distribution produced by Geosim. As you can see, it is not entirely different from the real thing!

In this case, I concluded that technological change together with strategic interdependence among the states were sufficient to generate the result, but there may well be other mechanisms that come closer to the truth.

Rem. Self-organized criticality has important consequences for theorizing about world politics. If it is true that warfare follows such a process, then the conventional focus on equilibria is misplaced, because warfare happens when the system is in transit from one equilibrium to another.

Let me now turn to more recent work. Having confirmed that war sizes are indeed power-law distributed, I got curious about territorial state sizes. Do they also exhibit patterns of the same type? Thanks to a new data set developed by colleagues in San Diego, I quickly found out that the answer to this question is no! In fact, state sizes are log-normally distributed.

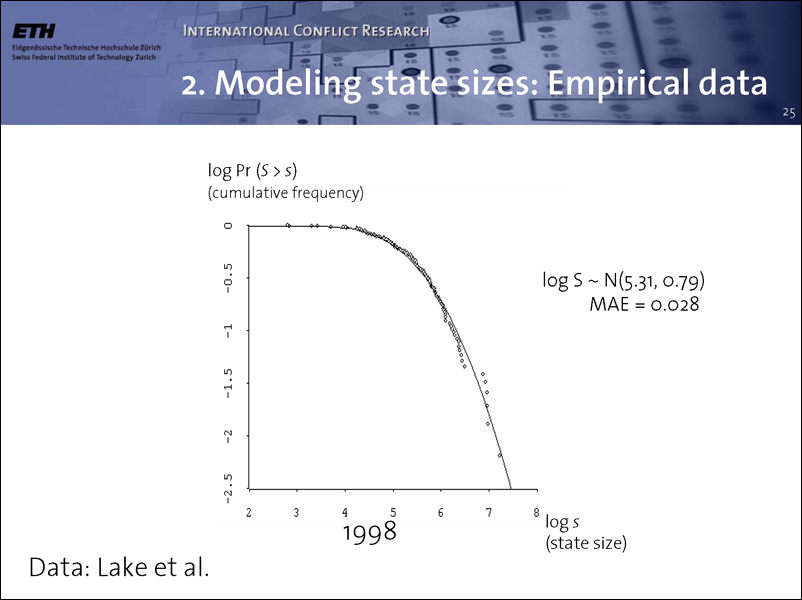
Here is a snapshot from 1998 that speaks a clear language. Had this configuration been power-law distributed, it should have appeared as a straight line in this doubly logarithmic diagram. In contrast, it is easy to fit a log-normal curve.

Again, we have to ask what mechanisms are responsible for this type of patterns. I ran Geosim with exactly the same configuration as the one used to produce war sizes, and the result was terrible. The simulated state sizes were simply too similar. It was not until I introduced mountainous terrain that realistic distributions started to appear.

Here is the system with rugged terrain marked in darker shades. In these areas, the capitals’ power extraction and projection are reduced.

As in European history, you can see that the largest states are located in the plains, whereas the smaller ones are mostly protected by the mountains.

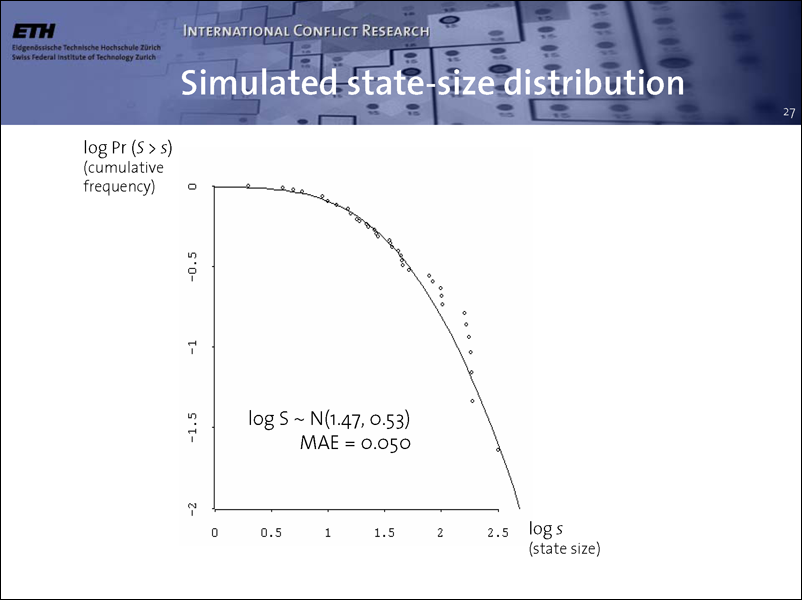
Here is a representative example of a simulated state-size distribution from this system. Though there are some deviations, the fit is not bad.

Of course, this does not mean that I have found the set of empirically accurate mechanisms. It merely says that this is a plausible set. Further experiments will be necessary to find robust answers to the question.

Let’s now lower our ambitions to a qualitative, rather than a distributional fit. How could one account for the extraordinary spread of democracy throughout the state system, starting with virtually no democracy in the late 18th century?

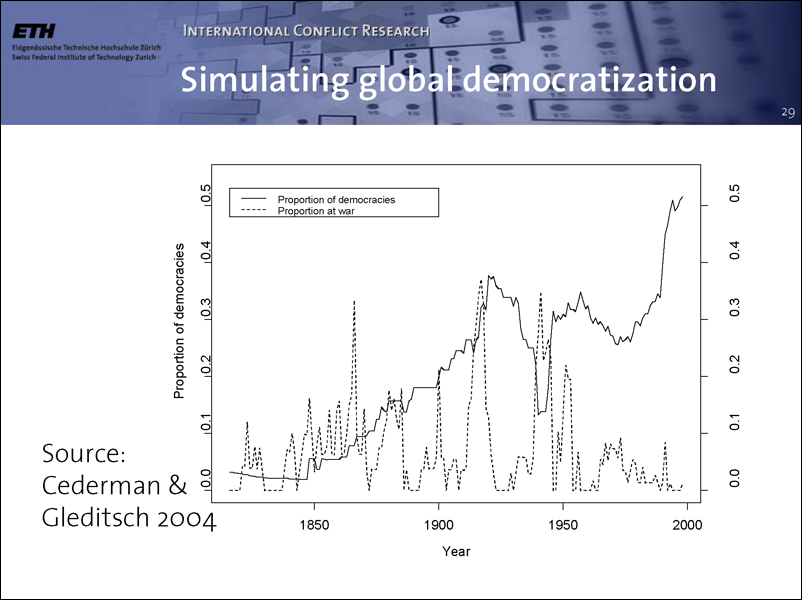
This chart traces the strength of democracy over time, measured by the proportion of democratic countries. The curve shows that the share of democratic states has increased from less than 5% at the starting point in 1816 to more than 50% at the present.

Despite being one of the most robust regularities to have been established in IR, the observation that democratic states rarely, if ever, go to war against one another remains a regularity in search of a theory.

Yet, the so-called democratic peace has rarely been theorized as a macro process, as it was by Immanuel Kant. In fact, the 18th century philosopher came up with one of the boldest predictions that I know of, and what’s more, he’s been proven right! Kant argued that democracy has the potential of taking off even in a harsh geopolitical environment.

To test Kant’s peace scenario, I introduced a new type of state. Shown in yellow are democracies as conditional cooperators, i.e. these states refrain from attacking each other, but otherwise have a healthy geopolitical appetite.

As shown by this sample run, local democratization together with a collective security mechanism is sufficient to democratize the entire system. Rerunning the system with random changes confirms that in most of the runs, the democracies dominate the final equilibrium.

Rem. This model serves as a corrective to the gloom and doom scenario of power laws. Indeed, by building up communities of trust and cooperation, democratic states seem capable of emancipating themselves from the iron law of geopolitics.

My final example is drawn from work that is still very much in progress. This is an attempt to extend Geosim to civil wars and nationalist insurgencies.

As wars among states become less frequent, academic attention has shifted increasingly to internal conflict. In recent years, an exciting literature on the causes of civil wars has emerged. For example, political economists have recently proposed models of insurgency that depend on states’ capacity to project power in rugged terrain rather than on ethnic allegiances.

Yet, a large gap remains between observed macro-level patterns and postulated rationalistic micro-level explanations.
Aiming to reproduce similar, qualitative process properties, this version of Geosim offers an alternative account that interprets insurgency as a process of identity-driven, nationalist mobilization leading to violence when the power balance favors peripheral communities over centers.

It is necessary to expand the Geosim framework by allowing provinces to challenge the authority of the centers. This is where cultural identities, relating to our third dimension of complexity, are brought into the picture. Thus this model features not only states and mountains, but also national identities.

To articulate such identity-based mechanisms, I have thus put together a very complex model that features state formation with cultural assimilation, as well as nationalist mobilization and nationalist insurgencies.

Rather than describing the model in the abstract, it is more instructive to view a brief movie illustrating a last sample run of the system.

>> Sample run 3

>> Shock and awe

>> As you can see, this is a 3D view of an artificial world. As before, state borders are marked with black lines, and here capitals are shown as black balls. The colored disks introduce the national identities that sometimes serve as platforms of insurrectional activity, which is shown as red bars.

>> Some states are almost perfect nation states in which the capital coincides with the dominant culture of the country. Others, however, are much more fragmented, as for example the one in the upper left corner.

>> It becomes evident that most of the violence happens in the mountains.

Using statistics, it can be shown that the findings of this model coincide with the results of conventional, materialist models, but unlike them, the current framework features explicit identities that open up windows of opportunity to rebellious groups.

Because of the extraordinary importance of nationalist insurgencies and failed states in the current world, the future work of our research group will revolve around this theme in the years to come. Unfortunately, we are unlikely to become unemployed for a long time.

The challenge will be to create more realistic models that will enable a much more precise evaluation of processes and policies. Having already established new contacts with empirical experts in the US and Scandinavia, we hope to integrate their deep knowledge within the modeling framework. This will include an effort to map out data with Geographic Information Systems, both in terms of the underlying geography and the ethnic maps involved.

Another parallel strategy will be to radically simplify the system in order to take advantage of analytical results from complexity theory.

Our International Conflict Research group still hasn’t reached its cruising altitude. The team remains “klein aber fein”:

Luc Girardin is our computer expert, and without his help, I would not have had any nice pictures to show.
Claudia Jenny runs our office and without her help there would not have been any invitations or apéro.

But we need to expand beyond that, so we will be hiring Ph D students, if possible already this summer. If you are interested in joining the team, or if you know someone who would like to do so, please look us up on the web. We welcome both natural and social scientists.

Still it would be a mistake to believe that ABM is limited to conflict. Quite on the contrary. The technique can be used in a wide variety of disciplines.

Catering to such a broad audience, we are already offering a lecture course on “Computational modeling of social systems” that is quite well attended, and in the future, we’re planning to offer similar courses every year for those who want to gear up.

Finally, with the generous support of ETH and in collaboration with David Lazer, at Harvard University, we will launch a new Transatlantic Initiative on Complex Organizations and Networks, or TAICON for short. This program includes lectures and workshops on computational and network related topics. Our first event will be a lecture on January 12 by the physicist Duncan Watts who works in the sociology department at Columbia University. I hope you will be able to attend our events.

And with this unashamed PR drive, I close my Einführungsvorlesung.